Doc Réduction d'endomorphismes

Réduction rationnelle des endomorphismes


Ce document traite de la réduction des endomorphismes sur un corps commutatif K tel qu'il a été enseigné à des étudiants de L3 en liaison avec des exercices interactifs.
On fixe un corps commutatif K et un espace vectoriel V de dimension finie n. On note EndK(V) l'ensemble des endomorphismes de E. Il est muni d'une structure d'algèbre ( K-espace vectoriel + anneau + compatibilité entre les lois).

I Polynômes d'endomorphismes

II Sous-espaces stables

III Sous-espaces cycliques

IV Dualité

V Facteurs invariants et décomposition rationnelle (Frobenius)

VI Diagonalisation et trigonalisation

VII Décomposition de Jordan

VIII Tous les exercices WIMS utilisés

I Polynômes d'endomorphismes

Réduction rationnelle des endomorphismes → I Polynômes d'endomorphismes
Si u est un endomorphsime de V et si P est un polynôme à coefficients dans K,, on définit P(u) comme l'endomorphsime de V suivant : si ,
où ( i fois).

Lemme

L'application définie par définit un homomorphisme d'algèbres.

Proposition

Le noyau de eu est un idéal de K[x] non réduit à . Note
cela signifie que si P et Q appartiennent à , si R appartient à K[x], si , appartient à , .

Démonstration
Le noyau de eu est un idéal car si P et Q appartiennent à , si R appartient à K[x],
  1. ;
  2. .

Les Id, u, ..., sont n2 + 1 éléments de l'espace vectoriel EndK (V) qui est de dimension n2. Donc, il existe des éléments a0, ... , de K non tous nuls tels que . Le polynôme est un polynôme non nul appartenant au noyau de eu.

Tout idéal de K[x] est principal, c'est-à-dire de la forme pour un polynôme .

Définition

On appelle polynôme minimal le générateur unitaire de l'idéal . On le note .
Le polynôme minimal est aussi le polynôme unitaire non nul de plus bas degré du noyau de eu.

Définition

On définit le polynôme par
où est une base quelconque de V et où est la matrice de u dans la base .
On déduit de la formule que ne dépend pas de la base. Ce polynôme est au signe près ce qui est appelé le polynôme caractéristique de u et nous l'appellerons ici le polynôme caractéristique de u.

Exemple

Soit u un endomorphisme tel que uk = 0 et pour un entier k > 0. Alors, , .

II Sous-espaces stables

Réduction rationnelle des endomorphismes → II Sous-espaces stables

Définition

Un sous-espace W stable par u est un sous-espace de V tel que .

Proposition

Soit W un sous-espace de V stable par u, alors divise , divise .

Démonstration
Pour le polynôme caractéristique, on écrit la matrice M de V formée d'une base de W complétée en une base de V. On doit alors calculer où MW et M2 sont des matrices carrées. Le déterminant se calcule alors par blocs{footnote} Si A est une matrice carrée de taille r, B une matrice carrée de taille s et C une matrice rectangulaire à r lignes et s colonnes,
{footnote}

Exemple

  1. Si P est un polynôme, et Im P(u) sont des sous-espaces stables pour u.
  2. Si D est une droite stable, il existe tel que pour tout . On a alors . En prenant pour P le polynôme minimal , on obtient que et donc que 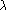lambda est une racine du polynôme minimal de u.

Théorème [Théorème des noyaux]

Soient P1, P2, ... , Pr des polynômes premiers entre eux dans leur ensemble. Alors
De plus, chacun des projecteurs correspondant à cette décomposition en somme directe est un polynôme d'endomorphismes en u.

Note
On dit que V est somme directe des sous-espaces vectoriels Vi si une des conditions équivalentes suivantes est vraie :
  1. tout vecteur de V s'écrit de manière unique sous la forme avec ;
  2. pour tout , et tout vecteur de V s'écrit sous la forme (autrement dit ) ;
  3. si fi est une famille d'applications linéaires de Vi dans un espace vectoriel W, il existe une unique application linéaire de V dans W coïncidant avec fi sur Vi.

En particulier, les projecteurs commutent avec u.
Démonstration
Démonstration pour deux polynômes. Si U1 et U2 sont deux polynômes de K[x] tels que U1 P1 + U2 P2 =1 et si , alors a= b + c avec et . Le projecteur de sur est donc donné par le polynôme d'endomorphisme ( U2 P2)(u). Il commute donc à u.

Exercice

Endomorphismes et projecteurs

Exercice

Polynômes d'endomorphismes et projecteurs

III Sous-espaces cycliques

Réduction rationnelle des endomorphismes → III Sous-espaces cycliques
Soit . Soit le sous-ensemble de V formé des vecteurs de la forme P(u)(a) pour . C'est un sous-espace vectoriel de Vu engendré par les ui(a) pour .
On note le polynôme unitaire engendrant l'idéal noyau de l'homomorphisme de K[x] dans V. C'est un diviseur de .

Proposition

Si d est le degré de , les vecteurs a, u(a), ..., forment une base de . Dans cette base, la matrice de est de la forme (cas où d=5)
avec .
Une telle matrice est appelée la matrice compagnon du polynôme . On la note C(P).

Définition

On dit que V est u-cyclique s'il existe tel que . Autrement dit, a, u(a), ..., est un système générateur de V.

Proposition

Le polynôme caractéristique d'une matrice compagnon est égal à son polynôme minimal.

Démonstration
On démontre la propriété par récurrence sur le degré de P. Si P est de degré 1, C(P) = det (x -a0) = x-a0.
On développe le déterminant de x Id - C(P) par rapport à la première colonne, puis le deuxième déterminant obtenu par rapport à la dernière colonne. On obtient
où .
ce qui est égal à x Q + (-1)5(-1)3 a0 = P.

Les deux lemmes suivants serviront à la démonstration de la proposition qui les suit.

Lemme

Soit et soit . On suppose que P = Q R avec Q unitaire. Alors, si b = Q(u)(a), .

Démonstration
On a R(u)(b) = P(u)(a)=0. Donc divise R. Si S(u)(b)=0, on a (Q S)(u)(a)=0, donc P=Q R divise Q S et R divise S. En appliquant à , on en déduit que R divise et finalement que .

Lemme

Soient a et b deux vecteurs de V. Alors si et sont premiers entre eux.

Démonstration
Posons et . Comme (P Q)(u)(a+b) =0, divise P Q. Soit R tel que R(u)(a+b) = 0. Alors,
Donc, Q divise P R. Or Q et P étant premiers entre eux, Q divise R par le lemme de Gauss. De même, P divise R. donc P Q divise R puisque P et Q sont premiers entre eux. En prenant , on en déduit le résultat.

On montre par récurrence que si a1, ... ar sont des vecteurs et que les polynômes sont premiers deux à deux, alors

Proposition

Soit u un endomorphisme de V.
  2. Il existe un vecteur tel que . Plus précisément, si est une base donnée, a peut être choisi dans cette base.

La proposition précédente est l'analogue des assertions suivantes dans un groupe abélien fini A : l'exposant de A est égal au ppcm des ordres des éléments de A et il existe un élément de A dont l'ordre égal à l'exposant de de A.
Démonstration
  1. Le polynôme divise pour tout vecteur a, donc divise . Réciproquement, prenons une base de V. Soit R le ppcm des . Si , , on a
    Donc divise R.
  2. Ecrivons la décomposition en éléments irréductibles de :
    avec les Pi premiers entre eux deux à deux. On a avec . Le polynôme minimal de la restriction de u à Vi est un diviseur de . Le polynôme minimal de est alors le produit des , mais il vaut aussi , ce qui prouve qu'en fait . Sur chacun des sous-espaces Vi (stables par u), prenons une base . Le ppcm des pour est égal à . Il existe donc un élément ai de telle que . Le vecteur vérifie alors , ce qui démontre la proposition.

IV Dualité

Réduction rationnelle des endomorphismes → IV Dualité

IV-1 Survol des propriétés de la dualité

IV-2 Dualité et sous-espace stable

IV-3 Exercices

IV-1 Survol des propriétés de la dualité

Réduction rationnelle des endomorphismes → IV Dualité → IV-1 Survol des propriétés de la dualité

Définition

L'espace dual d'un espace vectoriel V est l'espace vectoriel des formes linéaires sur V, c'est-à-dire l'espace vectoriel des applications linéaires de V dans K.
Si est une base de V, les formes coordonnées sont les formes linéaires

Proposition

Soit une base de V. Il existe une unique base de V (appelée base duale) telle que si i=j et 0 sinon.

Proposition

L'application donnée par est une application linéaire injective, bijective car V est supposé de dimension finie.

Définition

Soit , il existe un unique endomorphisme u de V tel que pour toute forme linéaire f.

Proposition

On a pour u et v appartenant à EndK(V) et ,

Proposition

On a . Autrement dit, si l'on identifie avec V via iV, s'identifie à u.

Démonstration
Soit . Alors, est un élément du dual de V. Si , on a
Donc pour tout et ^ i_V ).

Une notation agréable pour noter la dualité est d'écrire
Réécrivez la démonstration précédente avec ces notations.

IV-2 Dualité et sous-espace stable

Réduction rationnelle des endomorphismes → IV Dualité → IV-2 Dualité et sous-espace stable

Définition

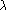Soit W un sous-espace de V. On appelle orthogonal de W et on note Wo le sous-espace de formé des formes linéaires lambda nulles sur W.

Proposition

Soit u un endomorphisme de V et W un sous-espace de V, alors son orthogonal Wo est stable par u.

Démonstration
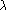Soit lambda une forme linéaire appartenant à Wo. Pour ,
puisque ( W est stable par u). Donc, est nul sur W et appartient donc à Wo.

Proposition

L'application donnée par avec est bien définie et est un isomorphisme.

Démonstration
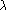D'abord est bien définie car . Montrons l'injectivité : si pour tout , alors aussi. Montrons la surjectivité : Soit une forme linéaire de dans K. Posons . Alors, on a évidemment pour et donc lambda appartient à Wo.

Proposition

On a .

Démonstration
On a
Pour démontrer la dernière égalité, choisissons un supplémentaire W' de W dans V, la projection est une application linéaire,
  • injective car ;
  • surjective car tout vecteur v est la somme d'un vecteur w' de W' et d'un vecteur w de W ;
donc un isomorphisme entre W' et . D'où

IV-3 Exercices

Réduction rationnelle des endomorphismes → IV Dualité → IV-3 Exercices

Exercice

Soient F et G deux sous-espaces vectoriels de V tels que . Montrer que .

Exercice


Soient V et W deux espaces de dimension finie et f une application linéaire de V dans W.
  1. Montrer que et que Solution
    Rappelons que t f est l'application linéaire de W dans V défini par avec et ou en utilisant la forme bilinéaire définie par ,
    On a alors les équivalences
    Donc si et si , on a , donc 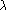lambda appartient à l'orthogonal de . On obtient donc l'inclusion .
    Réciproquement, on peut invoquer les dimensions. On peut aussi le faire ``explicitement'' : soit , on choisit un supplémentaire W1 de dans W. On définit si w=f(v) et si . Cette définition ne dépend pas du choix de v grâce à la propriété que si ) et définit une application linéaire. On a bien .
    ...

  2. Montrer que f est surjective si et seulement si t f est injective et que f est injective si et seulement si t f est surjective Solution
    Cela se déduit de la question précédente :
    f est surjective est injective.

Exercice


Soit f une application linéaire de V dans W. Soit X un sous-espace de V, Xo son orthogonal dans V. On note .
  1. Montrer que A est l'orthogonal de f(X) dans W.
    Solution
    .

  2. Si X et Y sont deux sous-espaces supplémentaires de V, montrer que Xo et Yo sont supplémentaires dans V.
    Solution
    Soit . Alors, pour tout , pour tout , et . Donc, comme X et Y sont supplémentaires, pour tout . Donc .
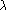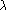    On peut ensuite invoquer les dimensions. Ou : soit . On définit comme l'unique forme linéaire coincidant aec lambda sur X et valant 0 sur Y et comme l'unique forme linéaire coincidant avec lambda sur Y et valant 0 sur X. On a bien . De plus, , puisqu'elle est nulle sur Y et de même .

V Facteurs invariants et décomposition rationnelle (Frobenius)

Réduction rationnelle des endomorphismes → V Facteurs invariants et décomposition rationnelle (Frobenius)

V-1 Le théorème des facteurs invariants

V-2 Quelques conséquences

V-3 Cas des dimensions 2, 3 et 4

V-4 Des exercices corrigés

V-5 S'exercer : Invariants, classes de similitude.

V-1 Le théorème des facteurs invariants

Réduction rationnelle des endomorphismes → V Facteurs invariants et décomposition rationnelle (Frobenius) → V-1 Le théorème des facteurs invariants

Théorème [Frobenius]

Soit V un espace vectoriel de dimension finie et u un endomorphisme de V. Il existe et des sous-espaces u-cycliques Vi non nuls de polynômes minimaux unitaires tels que
  2. .
De plus la suite des polynômes est unique.

Donnons déjà quelques conséquences :
  1. Le polynôme minimal de u est donné par : .
  2. Le polynôme caractéristique est le produit des : .
  3. Le polynôme est un multiple de ; c'est le théorème de Cayley-Hamilton : .
  4. Les polynômes et ont mêmes facteurs irréductibles, ce qui se traduit par

Démonstration [ Existence ]
Par récurrence :
  1. On choisit un vecteur a tel que .
  2. On cherche un supplémentaire W' de stable par u.
  3. On applique l'hypothèse de récurrence à W'.

Cherchons un sous-espace cyclique dans le dual V de V. Pour cela, prenons une forme linéaire varphi qui ne s'annule pas sur W et telle que soit égal à : par exemple, prenons varphi telle que , , , avec . Cela est possible car les vecteurs forment un système libre. {footnote} Trouver varphi revient à résoudre un système linéaire. {footnote} Calculons .
Si , on a et . Remarquons que si avec et , on a
et donc
Donc pour P de degré strictement inférieur à d, P(t u) est non nul. Donc . D'autre part, est un diviseur de . Tout cela implique que .
On a ainsi trouvé un sous-espace cyclique Y pour , qui est stable par de polynôme minimal .
Montrons que W est d'intersection nulle avec l'orthogonal Y0 de Y.
Soit b un élément de W. Il est de la forme b = P(u)(a) avec ou P=0. Supposons P non nul. Pour tout polynôme Q,
Supposons de plus que . Alors, comme est un élément de Y, on a
pour tout polynôme Q. Prenons . Dans ce cas, est non nul si P est non nul (c'est le coefficient dominant de P). Ce qui n'est pas possible. Donc P=0 ainsi que b.
Une fois démontré que , la comparaison des dimensions implique que . Et le sous-espace Y0 est stable par u.

Montrons maintenant l'unicité des éléments . Commençons par un lemme simple mais important.

Lemme


Supposons que V est somme directe de où W1 et W2 sont des sous-espaces stables par u. Alors, .
Attention, cela est faux sans la condition de stabilité. Par exemple, soit u de matrice dans une base (e1,e2). Prenons W=K e1 et W2=Ke2. On a u(W1)=u(W2).
Démonstration
Il est toujours vrai que u(V)=u(W1) + u(W2). Calculons l'intersection de u(W1) et de u(W2). On

Démonstration [ Unicité ]
Supposons qu'on ait deux décompositions d'invariants respectifs et . On a puisqu'ils sont tous deux égaux au polynôme minimal de u. Supposons qu'on ait montré que jusqu'à l'indice j-1, . On désire montrer que . On applique l'endomorphisme :
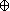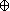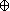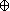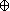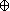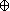   oplus      oplus      oplus  
   oplus      oplus      oplus  
(la somme reste directe d'après le lemme). Or annule Vk pour . Donc
   oplus      oplus     
   oplus      oplus      oplus     
Or les restrictions de u à Vi et à Vi' sont semblables pour i < j (même matrice dans des bases différentes). Il en est de même pour la restriction de u à et à pour i < j. On en déduit que et donc que est un multiple de . En échangeant les rôles, est aussi un multiple de et donc que .

Remarque

L'existence d'un supplémentaire stable par u d'un sous-espace vectoriel W stable par u n'est pas toujours vrai. Par exemple, prenons l'endomorphisme u de matrice dans une base (e1, e2). Le sous-espace est stable par u mais ne possède pas de supplémentaire stable par u. Sinon, u serait diagonalisable.

V-2 Quelques conséquences

Réduction rationnelle des endomorphismes → V Facteurs invariants et décomposition rationnelle (Frobenius) → V-2 Quelques conséquences

Proposition

Les endomorphismes u et ont même matrice dans des bases convenables.

Démonstration
Reprenons la démonstration du théorème.
  • Les restrictions de u à W et de u à Y ont même matrice dans les bases respectives et .
  • Wo s'identifie au dual de Yo grâce à l'application linéaire qui est une bijection (injection + même dimension). On a donc , et . On raisonne alors par induction.

Définition

Deux endomorphismes u et v resp de V et de V' sont dits semblables s'il existe un isomorphsime f de V dans V' tel que .

Théorème

Deux endomorphismes de V sont semblables si et seulement s'ils ont mêmes invariants (que l'on appelle pour cette raison, invariants de similitude).

Démonstration
Il suffit de remarquer que deux endomorphismes cycliques de même polynôme minimal sont semblables puisqu'ayant même matrice dans des bases convenables.

Proposition [Réduction de Frobenius d'une matrice]

Toute matrice est semblable à une matrice du type
avec . Et deux telles matrices sont semblables si et seulement si elles sont égales.
Réécrivons en proposition la caractérisation suivante d'un endomorphisme cyclique.

Proposition

L'espace vectoriel V est u-cyclique si et seulement si le polynôme minimal et le polynôme caractéristique de u sont égaux (ou ont même degré).

Démonstration
Nous avons déjà vu que si V est u-cyclique, on a . Réciproquement, supposons que . Il existe un vecteur a tel que est égal à . La dimension de est égale au degré de mu. La dimension de V est égale au degré de . Donc et .

Proposition [Cas particulier des endomorphismes nilpotents]

Soit u un endomorphisme nilpotent, c'est-à-dire de polynôme minimal égal à une puissance de x. Il existe des entiers (uniques) et une base tels que la matrice de u dans cette base doit de la forme
De plus avec .

La matrice C(xd) sera aussi notée J0(d), car c'est un cas particulier d'un bloc de Jordan.
La suite des forme une partition de d. On lui associe son diagramme de Young : la première ligne est formée de d1 cases, la seconde de d2 cases, ....
Le diagramme de Young représenté est associé à un espace vectoriel de dimension 11 somme directe de 4 sous-espaces u-cycliques. Ses invariants de similitude sont x4,x3,x2,x2.


V-3 Cas des dimensions 2, 3 et 4

Réduction rationnelle des endomorphismes → V Facteurs invariants et décomposition rationnelle (Frobenius) → V-3 Cas des dimensions 2, 3 et 4
Dans le cas de dimension 2 et 3, deux matrices sont semblables si et seulement si elles ont même polynôme caractéristique et même polynôme minimal.
    1. : nécessairement , la suite des invariants est .
    2. : nécessairement , la suite des invariants est .
    1. : nécessairement , la s.ite des invariants est .
    2. : nécessairement, avec et de degré 1 (il n'est pas possible que mu soit irréductible, car chi serait de degré 2 ou supérieur à 4 ...); on a , la suite des invariants est .
    3. : nécessairement, , la suite des invariants est .

Exercice

Dans le cas de dimension 4, trouver tous les types d'invariants de similitude possible selon les degrés et la décomposition en facteurs irréductibles du polynôme minimal. Vérifier que connaître le polynôme caractéristique et le polynôme minimal ne suffit pas à connaître la suite des invariants, donc la classe de similitude.
Solution
  1. : nécessairement , la suite des invariants est .
  2. et mu est irréductible : nécessairement , la suite des invariants est .
  3. et avec n'est pas irréductible :
    • soit et la suite des invariants est ;
    • soit et la suite des invariants est .
  4. et :nécessairement . Deux possibilités pour la suite des invariants :
    • soit la suite des invariants est ;
    • soit la suite des invariants est .
  5. et mu est irréductible : ce n'est pas possible.
  6. et avec : nécessairement , la suite des invariants est .
  7. et avec : nécessairement , la suite des invariants est .
  8. : nécessairement , la suite des invariants est .

V-4 Des exercices corrigés

Réduction rationnelle des endomorphismes → V Facteurs invariants et décomposition rationnelle (Frobenius) → V-4 Des exercices corrigés

Exercice


Soient P1, P2, P3 trois polynômes irréductibles distincts sur un corps K.
  1. Combien y a-t-il de classes de similitude de matrices à coefficients dans K ayant comme polynôme minimal P1 P22 P32 et comme polynôme caractéristique P13 P23 P34 ? Pour chacune d'elles, donner les invariants de similitude.
    Solution
    Les classes de similitude sont en bijection avec les suites de polynômes avec , et . Elles sont nécessairement de la forme
    avec et r1 + r2 + 1 = 3. D'où deux solutions :

  2. On prend et P1= x2 + 1, P2 = x+1 et P3=x-1. Parmi les classes de similitudes précédentes, quelles sont celles pour lesquelles la dimension de l'espace propre associé à la valeur propre 1 est supérieure ou égale à 3 ? Donner la matrice de Frobenius associée à une telle décomposition de Frobenius il ne doit donc apparaître que des matrices compagnons.
    Solution
    La condition impose que l'on est dans le premier cas. En effet, l'espace propre de u pour la valeur propre 1 restreint à chacun des sous-espaces cycliques est de dimension 1 si P3 divise le polynôme minimal de ce sous-espace cyclique et de dimension 0 sinon.
    P1 P22 P3=(x2+1)(x+1)2(x-1)= (x2+1)(x+1)2(x-1)=(x4-1)(x+1)=x5+x4-x-1, P1 P2 P3=x4-1 P1 P3=x3-x2+x+1. La matrice dans une base adaptée est alors

Exercice


Soit V un espace vectoriel de dimension finie et u un endomorphisme de V. On suppose que où les sous-espaces vectoriels Vi sont des sous-espaces stables par u, cycliques pour u de polynôme minimal respectif x, x, x(x-1), (x-1)2. Quelle est la dimension de V ? Donner les invariants de similitude de V et écrire une décomposition de Frobenius de u.
Solution
La dimension d'un espace cyclique est égale au degré de son polynôme minimal, puisque les polynômes minimal et caractéristique sont alors égaux. Donc V est de dimension 6. Soit . Comme les polynômes minimaux de V2 et V4 sont premiers entre eux, W1 est un espace cyclique de polynôme minimal (x-1)2 x. On a donc avec . Par unicité des invariants de similitude, ces invariants sont donc ( x(x-1)2, x(x-1), x).

Exercice


Soit V un espace vectoriel de dimension finie et u un endomorphisme de V. On suppose que le polynôme caractéristique de u est et que le noyau de u - 2Id est un plan. Quelles sont les formes possibles de la réduite de Jordan ?
Solution
Le nombre de blocs de Jordan correspondant à la valeur propre 2 est 2 car le sous-espace propre est de dimension. 2 Les formes possibles de Jordan sont donc (à permutation près des blocs sur la diagonale) ,

Exercice


Soit V un espace vectoriel de dimension finie et u un endomorphisme de V. On suppose que le polynôme caractéristique de u est et que le noyau de u - Id est un plan. Quelles sont les formes possibles de la réduite de Jordan ?à la valeur propre 1 est 2 car le sous-espace propre est de dimension 2. Les formes possibles de Jordan sont donc (à permutation près des blocs sur la diagonale)

V-5 S'exercer : Invariants, classes de similitude.

Réduction rationnelle des endomorphismes → V Facteurs invariants et décomposition rationnelle (Frobenius) → V-5 S'exercer : Invariants, classes de similitude.
Sous-espaces cycliques et invariants
Nombre de classes de similitude I
Nombre de classes de similitude II
Nombre de classes de similitude III

VI Diagonalisation et trigonalisation

Réduction rationnelle des endomorphismes → VI Diagonalisation et trigonalisation

Définition

Un polynôme de K[x] est dit scindé si c'est le produit dans K[x] de facteurs de degré 1.
Autrement dit, P est scindé s'il a toutes ses racines dans K.

VI-1 Endomorphismes diagonalisables

VI-2 S'exercer

VI-3 Endomorphismes trigonalisables

VI-4 Exercices

VI-1 Endomorphismes diagonalisables

Réduction rationnelle des endomorphismes → VI Diagonalisation et trigonalisation → VI-1 Endomorphismes diagonalisables

Définition

Un endomorphisme est diagonalisable si V admet une base formée de vecteurs propres de u.

Proposition

L'endomorphisme u est diagonalisable si son polynôme minimal est scindé et n'a que des racines simples.

Démonstration
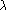Si u est diagonalisable de valeurs propres , , , (énumérées sans multiplicité), soit une base de vecteurs propres Alors, le polynôme annule u, c'est-à-dire que P(u) = 0 puisque si lambda est la valeur propre associée à ei. Donc qui est un diviseur de P est bien scindé et avec des racines simples (en fait, ).
Réciproquement, supposons que avec pour . Les polynômes sont alors premiers deux à deux et on peut appliquer le théorème du noyau :
(décomposition en sous-espaces stables par u). La restriction de u à étant une homothétie de rapport , u est diagonalisable.

Supposons u diagonalisable. Cherchons la décomposition de Frobenius de u. On a . Rappelons que et que le produit des doit être égal à ( ni est donc la multiplicité de dans ). La seule possibilité combinatoire est que
etc. Donnons une démonstration par récurrence plus constructive relativement à une décomposition en somme directe de sous-espaces cycliques en reprenant la démonstration générale de constructions des invariants. On sait qu'il existe un vecteur a tel que . Par exemple, on peut prendre où ai est un vecteur propre (non nul) de valeur propre . On sait alors qu'il existe un sous-espace W stable par u tel que . Le polynôme minimal de est un diviseur de , il est donc encore scindé et sans facteurs multiples. Donc est diagonalisable, on a et on applique l'hypothèse de récurrence.

Remarque

La généralisation naturelle de la notion de diagonalisable est la suivante. On dit que u est semi-simple si son polynôme minimal est un produit de polynômes irréductibles Pi où Pi et Pj sont premiers entre eux si . Dans ce cas-là, les invariants de u sont déterminés par le polynôme minimal et le polynôme caractéristique :
La démonstration est similaire.
On remarque que étant donné un polynôme sans facteur multiple (les Pi étant irréductibles) et un polynôme avec , il existe une unique classe d'endomorphismes semi-simples de polynôme minimal P et de polynôme caractéristique Q. L'unicité est bien sûr fausse si on enlève la condition semi-simple comme on l'a vu dans un cas de dimension 4.

VI-2 S'exercer

Réduction rationnelle des endomorphismes → VI Diagonalisation et trigonalisation → VI-2 S'exercer

Exercice

Diagonalisable ?
Trouver un vecteur propre
Matrice diagonalisable ?
Trouver un vecteur propre
Matrice diagonalisable ? Peut-on conclure
Petit QCM sur la diagonalisation

VI-3 Endomorphismes trigonalisables

Réduction rationnelle des endomorphismes → VI Diagonalisation et trigonalisation → VI-3 Endomorphismes trigonalisables

Définition

Un endomorphisme u est dit trigonalisable s'il existe une base de V dans laquelle la matrice de u est triangulaire.

Définition équivalente : Un endomorphisme u est dit trigonalisable s'il existe une suite de sous-espaces vectoriels Wi stables par u telle que avec .

Proposition

L'endomorphisme u est trigonalisable si et seulement si le polynôme est scindé (ce qui est aussi équivalent à ce que soit scindé).

Démonstration
Supposons u trigonalisable. En calculant le polynôme caractéristique de u dans une base dans laquelle la matrice de u est triangulaire, on voit que où les sont les éléments de la diagonale. Le polynôme minimal étant un diviseur de , il est lui aussi scindé.
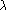Supposons maintenant que est scindé (et donc ). Le polynôme minimal de l'endomorphisme dual est lui aussi scindé. Donc, a un vecteur propre (non nul) varphi dans V de valeur propre lambda. Soit H le noyau de la forme linéaire varphi. C'est un sous-espace vectoriel de V de dimension n-1 (hyperplan) stable par u car est un sous-espace de V stable par : refaisons la démonstration : si ,
Soit D = K en un supplémentaire de H dans V. La matrice de u dans une base de la forme (base de H, en) est de la forme
On est ramené à étudier : le polynôme caractéristique de v est un diviseur de et est donc scindé (calcul dans la base précédente). On procède alors par induction.

VI-4 Exercices

Réduction rationnelle des endomorphismes → VI Diagonalisation et trigonalisation → VI-4 Exercices

Exercice


Dans les deux premières questions, u est un endomorphisme diagonalisable de V et S l'ensemble de ses valeurs propres. Pour tout , on note Vs l'espace propre associé.
  1. Montrer qu'un sous-espace W de V est stable par u si et seulement si W est somme (alors directe) des pour .
    Solution
    Le sous-espace propre Vs est le noyau de P(u) avec P le polynôme x-s. Si W est stable par u, il en est de même de . En particulier, les sous-espaces sont en somme directe. D'autre part, la restriction de u à W est diagonalisable (son polynôme minimal n'a que des zéros simples). Si Ws est l'espace propre de associé à la valeur propre s, on a . Donc .
    La réciproque est facile : il suffit de montrer que est stable par u. Or si ,

  2. En déduire que tout sous-espace de V stable par u possède un supplémentaire stable par u.
    Solution
    Soit W un sous-espace stable par u. Soit Ys un supplémentaire de dans Vs. Il est nécessairement stable par u, car la restriction de u à Ys est une homothétie. Alors est un supplémentaire de W dans V stable par u (on a , les dimensions sont OK et .


  3. Soit u un endomorphisme de V dont le polynôme caractéristique est scindé. Supposons que tout sous-espace de V stable par u ait un supplémentaire stable. Montrer que u est alors diagonalisable.
    Solution
    Supposons que u n'est pas diagonalisable. Il existe alors une valeur propre s et un vecteur v tel que (u-s Id)2(v)=0 et . Soit W le sous-espace engendré par w. Il est stable par u car u(w)=sw. Donc il admet un supplémentaire H stable par u. On décompose v= w' + h avec et . En appliquant u, u(v)=s v + w = sw'+sh + w ce qui vaut d'autre part u(w')+ u(h)=s w'+ u(h). Donc, u(h)=s h + w. Comme u(h) appartient à H, on en déduit que w appartient à H ce qui est impossible.

  4. Contre-exemple si u n'est pas diagonalisable.
    Solution
    Prenons u de matrice dans une base. Le sous-espace est stable par u mais ne possède pas de supplémentaire stable par u. Sinon, u serait diagonalisable.

VII Décomposition de Jordan

Réduction rationnelle des endomorphismes → VII Décomposition de Jordan

VII-1 Réduction de Jordan

VII-2 Formes de Jordan possibles

VII-3 Dimension de la somme des espaces propres

VII-4 Exercice : décomposition de Dunford explicitement

VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent

VII-6 Vecteurs propres, blocs de Jordan pour les endomorphismes nilpotents

VII-7 Quelques exercices

VII-8 Exercice : décomposition de Jordan-Chevalley

VII-9 Endomorphisme cyclique et commutant

VII-10 Carré d'un endomorphisme

VII-1 Réduction de Jordan

Réduction rationnelle des endomorphismes → VII Décomposition de Jordan → VII-1 Réduction de Jordan
On suppose désormais que u est trigonalisable, autrement dit que est scindé et on cherche une forme matricielle simple. On va déduire les résultats de ce qu'on a déjà démontré sans hypothèses sur (réduction de Frobenius).

Définition

On appelle bloc de Jordan associé à la matrice de taille r avec si i =j, si i = j+1 et 0 sinon. Exemple :
Autrement dit, est la matrice compagnon de xr. Elle est en particulier nilpotente. Le polynôme minimal de est xr. Le polynôme minimal de est . Remarquons que la matrice est semblable à la matrice compagnon du polynôme . En effet, si est la base dans laquelle on calcule la matrice compagnon de l'endomorphisme u, la matrice est la matrice dans la base (vérifier que c'est bien une base). En effet,

Théorème

Soit u un endomorphisme de V tel que est scindé. Il existe une base de V telle que la matrice de u dans cette base soit formée de blocs de Jordan sur la diagonale

Démonstration
On va le déduire du théorème de Frobenius. On va donner les étapes. On écrit , ,
  • décomposition primaire : ;
  • décomposition de Frobenius sur chacun des et de l'endomorphisme en somme directe de sous-espaces cycliques :
    avec un sous-espace cyclique de polynôme minimal , suite décroissante d'entiers avec . La matrice de u restreinte à dans la base est un bloc de Jordan de taille .

Théorème

Soit u un endomorphisme de V tel que est scindé. Alors, il existe deux endomorphismes s et n commutant tels que u = s + n avec s un endomorphisme diagonalisable et n un endomorphisme nilpotent. De plus s et n sont uniques et sont des polynômes en u.

Démonstration
Reprenons la démonstration précédente pour l'existence. Soit . C'est un endomorphisme nilpotent. On a . Notons n l'unique endomorphisme de V dont la restriction à Vi est ni et s l'unique endomorphisme de V dont la restriction à Vi est . On a bien u = s + n où s est diagonalisable et nilpotent.
Montrons que s commute avec u. En effet, soit pi les projections de V sur Vi. Les sous-espaces Vi étant obtenus par le théorème des noyaux, pi est un polynôme en u et . On en déduit que s commute avec u et n = u- s commute aussi avec u et avec s = P(u).
Montrons maintenant l'unicité. Ecrivons u = s + n = s' + n' avec s et n des polynômes en u. On en déduit que s' et n' commutent à s et n. Donc, s-s' est encore diagonalisable grâce au lemme qui suit et n - n' = s' - s étant à la fois diagonalisable et nilpotent est nul. Donc, n = n', s=s'.

Lemme

Deux endomorphismes diagonalisables et commutant possèdent une base commune de vecteurs propres.

Démonstration
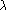Notons s et s' les deux endomorphimes. Soit lambda une valeur propre de s et . Montrons que est stable par s'. En effet, si ,
La restriction de s' à définit bien un endomorphisme de et est diagonalisable. Toute base de vecteurs propres de est aussi une base de vecteurs propres de . Il ne reste plus qu'à recoller puisque (car s est diagonalisable).

Exercice [ Et si les deux endomorphismes sont triangonalisables ]

Soient u et v des endomorphismes trigonalisables de V qui commutent. Montrer qu'il existe une base de V dans laquelle les matrices de u et v sont triangulaires. {sol} De manière générale, si Q est un polynôme, v laisse stable . En effet, si , on a Q(u)(v(x))=v(Q(u)(x))=0. Donc . Le polynôme caractéristique est scindé : avec les polynômes Pi premiers entre eux deux à deux et en fait de la forme . On a (théorème des noyaux). De plus, trouver une base dans laquelle la matrice de u est trigonalisable revient à trouver pour tout i, des bases compatibles des sous-espaces pour j variant. L'endomorphisme v laisse stable chacun de ces sous-espaces et est trigonalisable sur chacun de ces sous-espaces.
{sol}

VII-2 Formes de Jordan possibles

Réduction rationnelle des endomorphismes → VII Décomposition de Jordan → VII-2 Formes de Jordan possibles

Exercice

Quelles sont les formes de Jordan possible pour un endomorphisme de polynôme caractéristique (x+2)2(x-5)3 ?
Solution
On peut traiter indépendemment la partie (x+2)2 et (x-5)3 grâce à la décomposition en somme directe . La dimension de est 2 (car son polynôme caractéristique est (x+2)2.
Réduction de Jordan Nombre de blocs Invariants Diagramme de Young Dim de l'espace propre
2 (x,x) 2
1 (x) 1

La dimension de est 3 (polynôme caractéristique de degré 3).
Réduction de Jordan Nombre de blocs Invariants Diagramme de Young Dim de l'espace propre
3 (x,x,x) 3
2 (x2,x) 2
1 (x3) 1


On suppose de plus que l'espace propre associé à -2 est un hyperplan et que l'espace propre associé à 5 est un plan. Quelle est la réduction de Jordan ?
Solution
L'étude précédente montre que la réduction de Jordan est par exemple

Exercice

Matrices nilpotentes et tableaux de Young

VII-3 Dimension de la somme des espaces propres

Réduction rationnelle des endomorphismes → VII Décomposition de Jordan → VII-3 Dimension de la somme des espaces propres

Proposition

Supposons le polynôme minimal de u scindé. Supposons que avec semblable à un bloc de Jordan de valeur propre . Alors, la somme des sous-espaces propres de V est de dimension r.
Par exemple, si u a une seule droite propre, alors elle est semblable à un bloc de Jordan.

Exercice

Partitions et décomposition de Jordan

VII-4 Exercice : décomposition de Dunford explicitement

Réduction rationnelle des endomorphismes → VII Décomposition de Jordan → VII-4 Exercice : décomposition de Dunford explicitement

Exercice


Trouver la décomposition de Dunford de la matrice/endomorphisme .
Solution
On doit donc écrire u = s + n où s est diagonalisable, où n est nilpotente et où s et n commutent. On sait que s et n peuvent être obtenues comme un polynôme d'endomorphismes en u. Soit , . Le polynôme caractéristique de A est P1 P2. On a . Les projecteurs sur et sont donnés de la manière suivante : écrivons 1 = U P1 + V P2, alors tout vecteur a de V s'écrit sous la forme a = (V P2)(u)(a) + (U P1)(u)(a) ; le projecteur sur est donné par p1 = (V P2)(u) ; le projecteur sur est donné par p2 = (U P1)(u).
Alors, s=S(u) avec . On peut aussi écrire cela comme une solution du lemme chinois :
ou encore explicitement

On a
Donc
d'où
et
On trouve donc que
La matrice n se calcule par

Remarquons que si x=0, la matrice u est digonalisable et on a bien n=0 dans ce cas.

VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent

Réduction rationnelle des endomorphismes → VII Décomposition de Jordan → VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent

Soit V un espace vectoriel de dimension finie et u un endomorphisme.
  1. Soit W un sous-espace cyclique de V pour u de dimension d: il admet donc une base de la forme
    Soit f une forme linéaire ne s'annulant pas sur et s'annulant sur pour . Montrer que si Y est le sous-espace du dual de V engendré par , l'orthogonal Yo de Y est un supplémentaire de W dans V stable par u.
    Solution
    Montrons que Yo et W sont en somme directe. Soit un vecteur de W tel que t uj f(w)=0 pour tout j. Alors pour tout j. En prenant j=0, on obtient , puis avec j=1, , ... (système triangulaire).
    Montrons maintenant que Y est de dimension d. Dans le cas contraire, les formes linéaires seraient liées. Il existerait une combinaison linéaire nulle non triviale non nulle avec et . Donc sur le vecteur ,
    On a donc montré que . Le sous-espace Y est stable par t u. Donc son orthogonal Y0 est stable par u.

  2. Application : on considère l'endomorphisme u dont la matrice dans une base est

    On indique que le polynôme caractéristique de A est x5.
    1. Calculer la dimension des noyaux des puissances successives de u.
      Solution
      On calcule les puissances successives de A :

      Le noyau de u est de dimension 2 (on peut vérifier que le noyau de u est engendré par les vecteurs e2-e5 et e1-e2-e3-e4), le rang de u2 est 1. On en déduit que , , .

    2. En déduire la forme de Jordan de u (sans calculer de changement de base).
      Solution
      Le nombre de blocs de Jordan de taille supérieure ou égale à 1 est donc 2, le nombre de blocs de Jordan de taille supérieure ou égale à 2 est donc 4-2=2, le nombre de blocs de Jordan de taille supérieure ou égale à 3 est donc 5-4=1, le nombre de blocs de Jordan de taille supérieure ou égale à 4 est donc 0. Il y a donc un bloc de taille 2 et un bloc de taille 3 :

    3. En utilisant la méthode indiquée dans la première question, calculer une base dans laquelle la matrice de u est la matrice de Jordan trouvée à la question précédente.
      Solution
      On choisit un vecteur v1 tel que , par exemple dans les vecteurs de la base canonique. Prenons, v1 = e1. v2=u(v1)=e2-e3-2e4-2e5. On a alors v3=u2(v1)= -e1+e2+e3+e4. Soit . On cherche une forme linéaire f telle que et telle que f(u(v1))=0, f(v1)=0. Par exemple f = e2 + e3 : en représentant f par une matrice ligne : .
      On calcule une base du sous-espace cyclique Y engendré par f dans . On a
      L'orthogonal Y' de Y est un supplémentaire de W stable par u. Il est donné par les équations

      Une base de Y' est donnée par et . On doit maintenant choisir un vecteur dans Y' tel que . On prend . Soit . Dans la base (v1,v2,v3,v4,v5), la matrice de u est la matrice de Jordan écrite plus haut : si
      on a .

Exercice

Pratique de Jordan

VII-6 Vecteurs propres, blocs de Jordan pour les endomorphismes nilpotents

Réduction rationnelle des endomorphismes → VII Décomposition de Jordan → VII-6 Vecteurs propres, blocs de Jordan pour les endomorphismes nilpotents

On suppose désormais que u est nilpotent. On s'y ramène en utilisant le théorème des noyaux puis en étudiant plutôt que u. Soit xs son polynôme minimal.

Proposition

Soit u un endomorphisme nilpotent cyclique. Alors,

Démonstration
La dimension du noyau de u est de dimension 1 : pour cela, on travaille dans une base de Jordan. il s'agit de résoudre x1 = 0, ...., ; le noyau est donc engendré par le dernier vecteur de la base. Donc . La matrice de u2 est obtenue en mettant des 1 sur la deuxième diagonale inférieure. Son noyau est donc ...

On en déduit le cas général.

Théorème

Soit u un endomorphisme nilpotent d'invariants . Alors,
On peut aussi écrire que

Démonstration
On a avec Vi sous-espace u-cyclique de dimension ri. On déduit de la proposition précédente que .

On peut lire cette formule sur le diagramme de Young de u. Le terme est égal au nombre de lignes sur la k-ième colonne.


VII-7 Quelques exercices

Réduction rationnelle des endomorphismes → VII Décomposition de Jordan → VII-7 Quelques exercices

Exercice

Trouver les matrices A de taille 5, de rang 3, tel que le rang de A2 est égal à 1 et tel que A3=0.
Solution
On a , , . Le diagramme de Young est donc de la forme

Ses invariants sont (x3,x2).

Exercice

Soit K un corps commutatif. Combien y a-t-il de classes de similitude de matrices de M8(K) telles que ?
Solution
Une telle matrice est nilpotente et vérifie même A2 =0. Ses invariants de similitude sont .
On a , donc la dimension du noyau est 4. On en déduit que la suite des invariants est de longueur 4. La seule possibilité est donc qu'il y ait 4 blocs de taille 2. Son diagramme de Young est

Exercice

Soit K un corps commutatif. Combien y a-t-il de classes de similitude de matrices nilpotentes de M7(K) tel que ?
Solution
Une telle matrice vérifie A7 = 0. Ses invariants de similitude sont .
La dimension du noyau de A2 est égale à 3. On en déduit qu'il y a au plus 2 blocs (la dimension de ). Les diagrammes de Young possibles sont

Il y a trois classes de similitudes dont les invariants sont (x3, x3,x), (x4,x2,x), (x4,x,x,x).

Exercice

Soit K un corps commutatif. Combien y a-t-il de classes de similitude de matrices nilpotentes de M9(K) tel que rg A3 = 5 ? Pour chacune de ces classes, donner les invariants de similitude.
Solution
Les possibilités sont

Exercice


Soit la matrice .
  1. Montrer que A est nilpotente et calculer la dimension des noyaux des puissances successives de A. Donner la forme de Jordan J de la matrice A.
    Solution
    On a et A3=0. On voit des relations sur les colonnes de A : C1 = C3, C2+C3-C5 = C4. Donc l'image de A est engendrée par C1, C2, C4 et C6. On vérifie que ces quatre vecteurs forment un système libre (on peut aussi bien sûr résoudre directement les équations pour le noyau) : par exemple, si x C1 +y C2 +z C4 +t C5 = 0 en regardant l'avant-dernière ligne, on trouve que t=0. En regardant la troisième ligne, on en déduit que z=0, puis que x+2z=0, x-y=0, donc que la combinaison linéaire est triviale. Bref, .
    Passons à A2. Les colonnes 1 et 3 de A2 sont égales, les colonnes 4 et 5 sont liées. La dernière colonne est nulle. La somme de la deuxième colonne et de la troisième est liée à la quatrième ! L'image est engendrée par C1, C2 et on a .
    De ces informations, on déduit qu'il y a deux blocs de Jordan de dimension 3 chacun. On a donc

  2. Calculer une matrice inversible P (ou ) telle que .
    Solution
    On cherche une base dans laquelle la matrice de A est J. Pour cela, on choisit un vecteur tel que A2 = 0, par exemple, en notant ei la base canonique, v1= e1. On cherche alors une forme linéaire f telle que f(v1)=0, f(Av1)=0 et f(A2 v1)= 1. Par exemple, . L'orthogonal du sous-espace Y du dual engendré par f, f A et f(A2) f est un supplémentaire de <v1, A v1, A2 v1> stable par A. Calculons-le. On a , , L'orthogonal de Y est donc donné par les équations x5 = 0, x6=0, x1 + x2 + x3 = 0, dont une base est -e1 +e2, -e1 + e3. On vérifie que v4 = e2 - e1 est tel que . Donc la matrice A s'écrit J dans la base v1,A v1, A2 v1, v4,A v4, A2 v4, autrement dit si P=(v1,A v1, A2 v1, v4,A v4, A2 v4), on a .

Exercice

Soit V un espace vectoriel de dimension finie et u un endomorphisme dont la matrice est la suivante dans une base :
Répondre aux questions suivantes dans l'ordre désiré (en justifiant et en limitant les calculs) :
  1. Calculer le polynôme minimal de u.
  2. Ecrire la décomposition de Frobenius de V : en précisant la valeur de r et la valeur des polynômes minimaux de la restriction de u à Vi.
  3. Calculer la dimension des noyaux de us pour s entier.

Solution
On réécrit la matrice en faisant apparaître les blocs de Jordan :
Les polynômes minimaux des blocs de Jordan sont respectivement dans l'ordre x4, x3, x3, x, x, x2. Si on note Vi les sous-espaces vectoriels correspondant ( V1 est engendré par e1, ..., e4, V2 est engendré par e5, ..., e8, etc). Une décomposition de Frobenius de V pour u est donc . Le polynôme minimal de u est x4. Ses invariants de similitude sont (x4, x3, x3, x2, x, x). Le nombre de blocs de Jordan de taille supérieure ou égale à i est égale à . On en déduit que , , , .

Exercice

Matrice de Jordan et noyaux itérés
Partitions et décomposition de Jordan
Jordan et invariants de similitude

VII-8 Exercice : décomposition de Jordan-Chevalley

Réduction rationnelle des endomorphismes → VII Décomposition de Jordan → VII-8 Exercice : décomposition de Jordan-Chevalley

Soit A une matrice de polynôme caractéristique p et soit p1 la partie « sans facteur carré » du polynôme p, c'est-à-dire le quotient de p et de son pgcd par le polynôme dérivé p' de p.
  1. Soit s un polynôme vérifiant et . Montrer que le polynôme minimal de S = s(A) divise p1 et que A-S est nilpotente et commute avec S.
    Solution
    Les congruences se traduisent par s = x + q1 p1 et p1(s) = q2 p avec deux polynômes q1 et q2. Comme p est le polynôme caractéristique de A, on a p(A)=0, donc p1(S)=p1(s(A))=0, ce qui signifie que le polynôme minimal de S divise p1 et que S est semi-simple (diagonalisable sur ) puisque p1 n'a que des facteurs simples. D'autre part, S - A = q1(A) p1(A). Il existe une puissance p1n de p1 qui est divisible par p. Donc (S-A)n = q1(A)n p1(A)n=0 et S-A est nilpotente.

    La décomposition A = S + N est la décomposition de Dunford (Jordan-Chevalley) de la matrice A.
  2. Montrer qu'il existe un polynôme d1 tel que .
  3. Soit q un polynôme. Montrer que .
  4. On considère la suite de polynômes définis par s0=x, sn est le reste de la division euclidienne par p de (si q1, q2 sont deux polynômes, q1(q2) est le composé de polynômes ). Montrer que , puis que .
    En déduire que pour n assez grand, s=sn vérifie et (donner une estimation d'un tel n).
    Solution
    On a en utilisant la formule de Taylor que
    On en déduit par récurrence que
    En prenant 2n supérieur à un entier N tel que p1N soit divisible par p, on en déduit que . On vérifie alors par récurrence que . doit convenir.

  5. On prend p = (x2+x+1)3(x2+1)2 et A une matrice de polynôme caractéristique égal au polynôme p. Que vaut p1 ? Combien de termes de la suite doit-on calculer a priori pour trouver les matrices S et N de la décomposition de Dunford de A ? Il n'est pas demandé de faire le calcul, mais de dire quelles opérations seront faites.
    Solution
    On a p1=(x2+x+1)(x2+1). Comme p13 est un multiple de p1, . Donc il suffit de calculer s2. s1 = x-p1 d1, s2 = s1 -p1(s1) d1(s1).

Exercice

Pratique de la décomposition de Jordan-Chevalley

VII-9 Endomorphisme cyclique et commutant

Réduction rationnelle des endomorphismes → VII Décomposition de Jordan → VII-9 Endomorphisme cyclique et commutant

Proposition

Un endomorphisme u est cyclique si et seulement si les endomorphismes commutant avec u sont de la forme P(u) avec .

Démonstration
De manière générale, les endomorphismes de la forme P(u) commutent avec u.
Supposons que u est cyclique. Il existe donc tel que . Soit v un endomorphisme commutant avec u. Le vecteur v(a) s'écrit P(u)(a) avec puisque V est u-cyclique. Si , on a b=Q(u)(a) et
Donc v = P(u).
Supposons que les endomorphismes commutant avec u sont de la forme P(u).
Supposons que V n'est pas u-cyclique. On a alors une décomposition avec W stable par u avec . La projection p de V sur W parallèlement à commute avec u. En effet, si et , alors et et
Donc . Par hypothèse, il existe tel que p= P(u). On a p(a)=0=P(u)(a) donc P est un multiple de . On en déduit que P(u)(c) est nul pour tout et p(c)=0. Donc W=0.

VII-10 Carré d'un endomorphisme

Réduction rationnelle des endomorphismes → VII Décomposition de Jordan → VII-10 Carré d'un endomorphisme

Exercice

Carré d'un endomorphisme nilpotent

Exercice



Soit V un espace vectoriel de dimension finie n et u un endomorphisme de V nilpotent et cyclique. Montrer que avec V1 et V2 deux sous-espaces vectoriels cycliques pour u2 de dimension respective (entier inférieur le plus proche de ) et (entier supérieur le plus proche de ).
Solution
Soit v = u2. On a . Comme V est u-cyclique et que u est nilpotent, on a pour . On en déduit que . Donc v est la somme de deux blocs de Jordan. On a ensuite , ..., si . Les blocs de Jordan sont donc de taille et .

Soit A une matrice d'invariants de similitude (x5,x3,x,x).
  1. Donner les invariants de similitude de A2.
    Solution
    La matrice A est nilpotente. Les dimensions successives des noyaux de A sont 4, 4+2=6, 6+2=8, 8+1=9, 9+ 1=10. Les dimensions successives des noyaux de A2 sont 6, 9, 10. La suite des est 6, 3, 1. Les invariants de similitude de A2 sont (x3,x2,x2,x,x,x) (question précédente appliquée à chacun des sous-espaces cycliques pour A ou directement (3 = nombre de blocs de Jordan ; 2 = nombre de blocs de Jordan de taille , 2 = nombre de blocs de Jordan de taille , 1 = nombre de blocs de Jordan de taille , 1 = nombre de blocs de Jordan de taille , 1 = nombre de blocs de Jordan de taille .
    On peut le voir plus facilement à l'aide des tableaux de Young :
    A :
    A2 :

  2. Existe-t-il une matrice B non semblable à A dont le carré est semblable à A2 ? Si oui, en donner les invariants de similitude.
    Solution
    La matrice d'invariants de similitude (x5,x3,x2) convient.

    On peut vérifier que ce sont les seuls invariants de similitude possible (cela se voit facilement en utilisant les diagrammes de Young).

VIII Tous les exercices WIMS utilisés

Réduction rationnelle des endomorphismes → VIII Tous les exercices WIMS utilisés
Les exercices suivants se trouvent aussi au cours du texte.
  • Endomorphismes et projecteurs
  • Polynômes d'endomorphismes et projecteurs
  • Sous-espaces cycliques et invariants
  • Nombre de classes de similitude I
  • Nombre de classes de similitude II
  • Nombre de classes de similitude III
  • Diagonalisable ?
  • Trouver un vecteur propre
  • Matrice diagonalisable ?
  • Trouver un vecteur propre
  • Matrice diagonalisable ? Peut-on conclure
  • Petit QCM sur la diagonalisation
  • Matrices nilpotentes et tableaux de Young
  • Partitions et décomposition de Jordan
  • Pratique de Jordan
  • Matrice de Jordan et noyaux itérés
  • Partitions et décomposition de Jordan
  • Jordan et invariants de similitude
  • Pratique de la décomposition de Jordan-Chevalley
  • Carré d'un endomorphisme nilpotent

document sur la réduction rationnelle des endomorphismes.
: endomorphism_reduction, réduction de frobenius, triangonalisation, réduction de jordan, interactive mathematics, interactive math, server side interactivity

The most recent version
Cette page n'est pas dans son apparence habituelle parce que WIMS n'a pas pu reconnaître votre navigateur web.
Afin de tester le navigateur que vous utilisez, veuillez taper le mot wims ici : puis appuyez sur ``Entrer''.

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.