Calculs avec la loi normale
Introduction
La fonction de répartition de la loi normale centrée réduite est notée
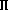, et ses valeurs se lisent dans la table du formulaire.
Les calculs peuvent se répartir en deux catégories :
- On cherche à calculer une probabilité ; dans ce cas, on aura besoin, au cours du calcul, de faire une lecture directe de la table
- On connait une probabilité, et on cherche ... autre chose (très varié !) ; dans ce cas, ce sera une lecture inverse de la table.
On cherche une probabilité
Lecture directe de la tableSi
T est une variable aléatoire suivant la loi normale centrée réduite :
(0,1), on a :
Loi normale centrée réduite ; calculs utilisant la lecture directe de la table
Les calculs concernant toutes les lois normales se font tous en se ramenant à la loi normale centrée réduite.
En effet, si
X suit la loi
(m,
), alors
suit la loi
(0,1).
Loi normale ; calculs utilisant la lecture directe de la table
On connait une probabilité et on cherche autre chose...
Lecture inverse de la tableLoi normale centrée réduite ; calculs utilisant la lecture inverse de la table
Loi normale ; calculs utilisant la lecture inverse de la table
Synthèse
Exercice de type BTS
Lecture directe de la table
Valeurs positives
On trouve donc :
Valeurs négatives
On utilise la symétrie de la courbe de densité de la loi normale, ce qui donne :
La valeur de se trouve dans la table à l'intersection de la ligne 1.6 et de la colonne 0.06.
On trouve donc :Loi normale centrée réduite (calculs directs)
Formules à utiliser :
==
=
=
=
Exemples de calculs variés
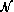(0 ; 1). Calculer
p(T < -0.13)
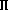(-0.13) = 1 - 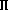(0.13) = 0.4483
Loi normale (calculs directs)
Principe de base :
On introduit la variable aléatoire T définie par :
qui suit la loi normale centrée réduite.
On traduit la question pour obtenir le calcul d'une probabilité concernant T, et on est donc ramené au cas précédent.
Exemples de calculs variés
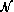(242 ; 11).Calculer P(X > 238.37)
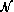(242 ; 11), donc la variable aléatoire T définie par :
suit la loi normale centrée réduite.
P(X > 238.37) =
P(T > -0.33) = 1 - 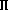(-0.33) = 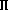(0.33) = 0.6293
Lecture inverse de la table
donné (compris entre 0 et 1).Il s'agit donc d'une lecture "inverse" de la table. Celle-ci se fait différemment selon que la valeur de est comprise entre 0 et 0.5 ou entre 0.5 et 1.
avec compris entre 0.5 et 1
On trouve dans la table :
et
.
0.62 est compris entre 0.5 et 0.8413, mais plus proche de 0.6915.
On prendra donc
h = 0.5.
On trouve dans la table :
et
.
0.94 est compris entre 0.5 et 0.8413, et est exactement au milieu entre ces deux nombres.
On prendra donc
h = 1.555.
avec compris entre 0 et 0.5
On utilise la symétrie de la courbe de densité de la loi normale, ce qui donne :
On cherche donc le nombre 1 - 0.38 = 0.62.
On a en effet :
On trouve dans la table :
et
.
0.62 est compris entre 0.5 et 0.8413, mais plus proche de 0.6915.
On prendra donc
- h = 0.5, d'où
h = - 0.5.
Loi normale centrée réduite (calculs avec lecture inverse)
Exemples de calculs variés
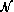(0 ; 1). Déterminer
a pour que :
P(T > a) = 0.8159
En appliquant la formule p(T > a) = 1 - 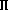(a), on obtient :
1 - 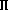(a) = 0.8159.
D'où
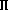(a) = 0.1841
Comme 0.1841 < 0.5, on cherche dans la table en lecture inverse le nombre
1 - 0.1841 = 0.8159.
On lit :
et finalement
a = -0.9
Conclusion : P(T > -0.9) = 0.8159
Loi normale (calculs utilisant la lecture inverse de la table)
Exemple de calcul où on cherche une borne de l'intervalle (ou les deux)
Déterminer h pour que P(X < h) = 0.98
D'après l'énoncé, P(X < h) = 0.98
On obtient donc en soustrayant 367 puis en divisant par 2.3 : .
On en déduit que .
Par lecture inverse de la table, on obtient alors :
et enfin :
Conclusion : P(X < 368.15) = 0.98
Exemple de calcul où on cherche la moyenne de la loi de X
Déterminer m pour que P(X < 383.7) = 0.79
D'après l'énoncé, P(X < 383.7) = 0.79
On obtient donc en soustrayant m puis en divisant par 1.4 : .
On en déduit que .
Par lecture inverse de la table, on obtient alors :
et enfin : d'où m = 383
Conclusion : Si X suit la loi normale de moyenne m = 383 et d'écart-type , on a P(X < 383.7) = 0.79
Exemple de calcul où on cherche l'écart type de la loi de X
.
Déterminer
pour que
P(X > 347.95) = 0.66.
, donc
suit la loi normale centrée réduite.D'après l'énoncé, P(X > 347.95) = 0.66
On obtient donc en soustrayant 344 puis en divisant par
:
, c'est à dire
.Ceci donne , d'où
Par lecture inverse de la table, on obtient alors :
et enfin :
d'où
Conclusion : Si X suit la loi normale de moyenne m = 344 et d'écart-type , on a P(X > 347.95) = 0.66
Exercice